[mathjax]
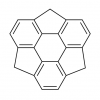
バックミンスターフラーレンC60の構造式を描くにあたって、フラーレンの基礎について学びます。私はフラーレン初心者なのでここに書いてあることはフラーレンにかかわっている方にとっては簡単すぎる内容だと思います。
まず、下記のことは既知とします。
→球のオイラー数は2であることが数学的に証明されている。
・5員環・6員環のみから成る。
・各炭素からは単結合2本、二重結合が2本伸びている。
これらを用いて5員環・6員環の数を確かめます。
$$x:5員環の数、y:6員環の数、v:頂点の数、e:辺の数、f:面の数とすると$$
$$v – e + f =2tag{1}$$
$$v = frac{5x + 6y}{3}tag{2}$$
$$e = frac{5x + 6y}{2}tag{3}$$
$$f = x + ytag{4}$$
$$v = 60tag{5}$$
$$が成り立つ。これを解いてx = 12、y = 20となる。$$
式(2)は単純に5・6員環の頂点の数をカウントするとトリプルカウントになるので3で除し、式(2)は同様に辺の数でダブルカウントになっている部分を2で除しています。
上記よりC60には5員環が12個、6員環が20個あることがわかります。このあたりのことは基本的すぎるためか、ネット上にはあまり詳しく説明している資料が見つかりませんでした。本を読んだ方が効率よさそうです。
ここで冒頭で挙げた3つの既知の事柄に加えて、下記を既知とします(これはどうやって証明するんだろう)。
これを用いれば、5員環を中心として周りに5員環同士が隣り合わないように6員環を配置した下記の構造が基礎になりそうなことが予想できます。これがコランニュレンですね。
ちなみにコランニュレンは下記のような二つの共鳴構造を描くことができます。5員環の2重結合の数が違いますね。
これについては大阪経済大学の西山豊先生の説明が非常にわかりやすいです。
(P11あたりからが該当)
またChem-Stationさんの記事によると芳香環の表記法についてはかなりこだわりがある人がいるようですが、深入りするのはここでは避けます(時間がとられるので手を抜きます)。
コランニュレンは5員環1つに対して6員環が5つ隣接しているので、これを5員環の数である12ユニット並べると単純に6員環の数は5*12=60となり、先の計算の6員環数20の3倍となってしまいます。このことから3つの5員環で1つの6員環を共有していることがわかり、上記コランニュレンにこのことをくわえると下記の構造になります。
5員環数6、6員環数10なのでこのユニットを単純に2つ合体させればバックミンスターフラーレンC60の完成です。
これをこうして
こうすると
フラーレンの完成です!
えっ?こんなのフラーレンじゃない?そんなことはありません。
これでC60フラーレンの完成です!
おまけ
http://kiriyamadouro.esy.es/kagoubutsu_bot/C60/C60.htm
佐藤健太郎先生の有機化学美術館というHPをボーっと読み返していると「続・フラーレンの話」というページのC200・ドーナツフラーレンが目にとまりました。
非常に興味深い形状をしているので、3Dでみるとどのような形なのだろうか気になり、3Dモデルを探したのですがめぼしいモデルは見つかりませんでした。
なので自分でC200・ドーナツフラーレンの3Dモデルを作成したのですが、その時に参照したページの備忘録を残しておきます。
ちなみに私はフラーレンを実験的に扱ったことはありません。
キーワードは「fullerene・donut・toroidal・topology・torus・heptagon」等。
「続・フラーレンの話」には
とあることから、このC200・ドーナツ型フラーレンは7員環を含むことがわかります。しかし、HP文章・画像からは7員環をいくつ・どの位置に含むかは不明です。さらに言えば5・6員環の数も不明です。
ところで建築家・発明家の阿竹克人さんという方のブログでこのフラーレンの実物モデルを組んでいました。あたけぼねとかベンデグリティーとかいうらしいです。
名古屋工業大学のトポロジーの専門家の平澤 美可三先生が関わっているらしいので、トポロジーが苦手な私にとって大変参考になります。
ふむふむ、トーラスのオイラー数は0なのか。ということは
$$x:5員環の数、y:6員環の数、z:7員環の数、v:頂点の数、e:辺の数、f:面の数とすると$$
$$v – e + f = 0tag{1}$$
$$v = frac{5x + 6y + 7z}{3}tag{2}$$
$$e = frac{5x + 6y + 7z}{2}tag{3}$$
$$f = x + y + ztag{4}$$
$$v = 200tag{5}$$
$$が成り立つ。これを解くとx = z、2x + y = 100となる。$$
つまり5員環と7員環の数は同じであり、5員環の数が増えるにしたがって6員環の数が減ることがわかります(当たり前ですが)。
x, y, zについては自然数であるという制約しかないので49通りの5・6・7員環の数が考えられます。
これ以上の制約条件としては構造の安定性を考慮するのでしょうが、よくわからないので今回はとばします(上記ブログの辺300というのはこれを取り入れているのか?)。
仮にx=5とすると(5員環10, 6員環80 , 7員環10)になります。この値を使ってまずは5員環1 ,6員環8, 7員環1の基本ユニットを作って、それを10個つなげていこうという方向性にしました。
しかしながら上記HPの画像だけではいまいち配置の方法がよくわかりません。なんとなく、7員環を上部・下部に5ずつ配置するんだろうという想像はつきますが・・・
ビーズの多面体で有名な堀部和経先生の下記リンクの92番のモデルが参考になりました。
(5員環12, 6員環60, 7員環12)のこのモデルではドーナツ内側の円の上部下部にそれぞれ6個の7員環が配置しているので、これを上部下部それぞれ5個に減らせば良いのだと推測できます。これに限らず様々なフラーレンのビーズモデルが載っていて面白いです。
本当は特殊な図形を描いていくのが正しいんでしょうが(ポワンカレの円板モデル?)、3Dモデルを早く作成してみたいので、早速モデル作成にとりかかりました。
まずは2D化学構造式エディタで5員環1, 6員環8, 7員環1の基本ユニットを作成する。これだけでいくつも候補があるのですが、やっていく内にコツが掴めてどのような組み合わせにすればわかってきました(説明できませんが・・・)。
そしてこれを2つ用意してつなげます。最終的に構造最適化をかけるので歪みは気にしない。
さらにどんどんつなげていき、5×2=10個の7員環を含む形にします。
次に側面同士をつなぎ最後に上部下部を繋ぎます。
これもうわかんねぇな。でも構造最適化すれば大丈夫!

http://kiriyamadouro.esy.es/kagoubutsu_bot/C200/C200.htm
3Dモデルで最初から作ればいいじゃんと思う方もいらっしゃるかもしれませんが、方向性がわかったら2Dで作れるところまで作っておくのが効率的だと思います。実際3Dで作ろうとして挫折しました。
・参考になった気分になれる折り紙のページ
・フラーレン生成プログラムとライブラリ
Centre for Theoretical Chemistry and Physics
→一般的なフラーレンやCNTのモデルはこれで作れるんでしょうが、導入が面倒なのと一般的ではないモデルを作成したいので見送り。
・ドーナツ型フラーレンについて参考になる日本人の論文
Toroidal form of carbon C360
Phys. Rev. B 47, 1703(R) ? Published 15 January 1993
Satoshi Itoh, Sigeo Ihara, and Jun-ichi Kitakami
http://dx.doi.org/10.1103/PhysRevB.47.1703
Toroidal forms of graphitic carbon
Phys. Rev. B 47, 12908 ? Published 15 May 1993
Sigeo Ihara, Satoshi Itoh, and Jun-ichi Kitakami
http://dx.doi.org/10.1103/PhysRevB.47.12908
・全くの素人の私にも参考になる総説。
http://iopscience.iop.org/1367-2630/5/1/126/fulltext
2003 New J. Phys. 5 126
Humberto Terrones and Mauricio Terrones
http://dx.doi.org/10.1088/1367-2630/5/1/126
Fig 26. (a)がまさにそれ。
フラーレンの模型を作っている方のブログ。
http://thebeadedmolecules.blogspot.jp/2010_11_01_archive.html
吉田満帆博士
コンピューターグラフィックで見るC60とその仲間たち,化学同人,1983
平成7年度博士(工学)の学位 豊橋技術科学大学